What are Markov Models?

 Markov Models stem from a branch of mathematics called Stochastic Processes, these are defined as a family of random variables. A Markov Model is a Stochastic method for modelling a randomly changing system in which the probability of an event is based on the historical data of past events, this can then be simulated with a Monte-Carlo algorithm.
 
 They were first defined by the Russian mathematician Andrey Andreyevich Markov (1856-1922) over 100 years ago, with his findings officially published in 1913 to the Imperial Academy of Sciences in St. Petersburg. He is credited with moving the idea of probability from situations such as dice rolling where each event is independent, towards a new school of thought of linking past events together to predict future ones.
 
 

 This was first known as a Markov Chain, a visual representation of the model showing the pathways a series of events could take where each chain between independent events was the probability of it occurring. The first analysis Andrey performed was on Pushkin's Poetry where each independent event was a word, and the relationships between them created the chains.

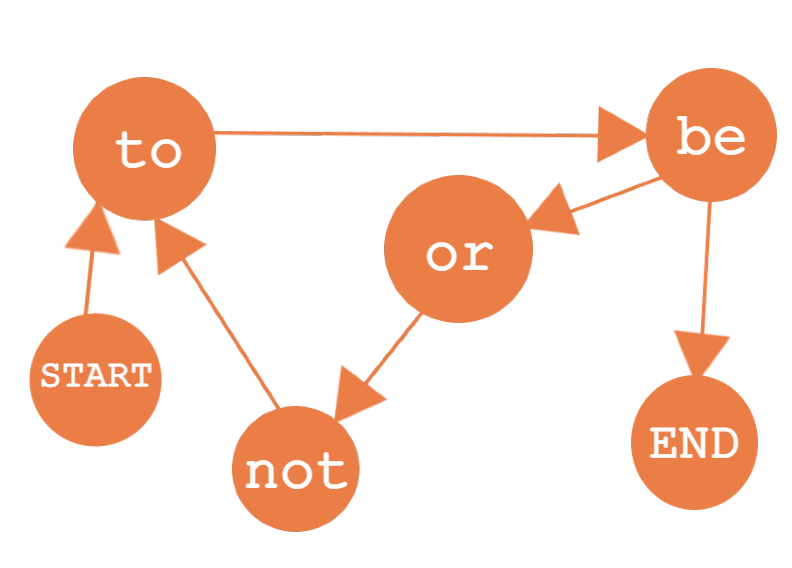
 Though Markov gained no new real insight into the poetry or its meaning, he did accidentally create one of the first machine learning based algorithms for text-data mining. Take the figure depicting the Markov Chain for the short quote "to be or not to be", it shows all the permutations the sentence could take if only the previous word is taken into account. With enough sentences, or data, the probabilities that the output simulated sentences make sense and are grammatically correct increases, a technique modern bots use when crawling through social media.

How do they work?

 Building a Markov Model is a relatively simple process. It starts with extracting all the unique events in a dataset, and building a scoring matrix with the unique events populating both the rows and the columns. For a first order model, only one matrix is necessary as we are only looking at one previous event to predict the next one. Running through the dataset sequentially, for each unique event increase the score in the cell where the column index is the current event and the row index is for the event prior.

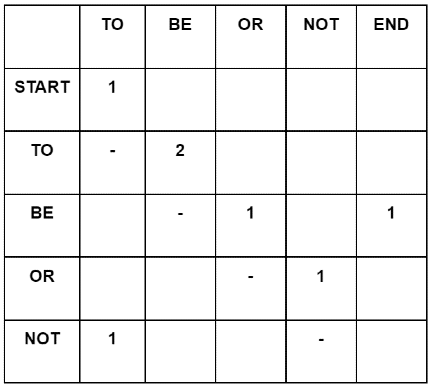
 Each row then represents the ratio of probability of the next event given the current event row index has occurred. If we were to run through the example with the word based dataset "to be or not to be" we would see at the start there is only the possibility for the word "to" to be the next possible event. Moving to the row index for "to", the only possible next word is "be" with 2/2 (100%) of the votes. The row index for the word "be" however has a 50% next event chance of either terminating, or the word "or". In a Monte-Carlo simulation, one way to choose would be to populate an array with all the next possible events, some of them duplicated to represent their frequency, and randomly choose an index. Though memory intensive, it's a simple and elegant solution for small datasets.

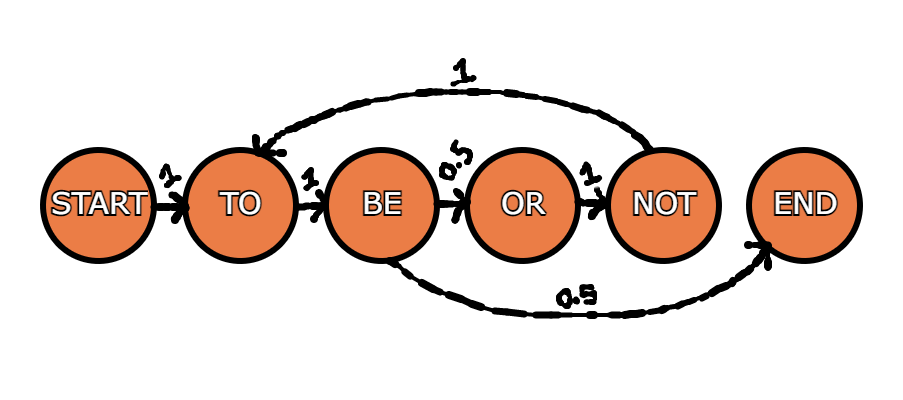
 Possible outputs for this example would be: "to be", "to be or not to be", "to be or not to be or not to be", and so on.

An Example with Words

 Lets put this into practise in the same way Markov did over 100 years ago with some poetry. I'm going to use the well known poem 'The Raven' by Edgar Allen Poe, though for simplicities sake I will be editing the punctuation down to just commas and full stops.

Read 'The Raven' Here

 As for programming language, I'll be using R for its native data frame handling. Reading the data in and splitting the full text into an array of both words and punctuation in sequential order, there are 1273 independent events with which to build this model. Using the "unique()" function, it can be determined there are 439 distinct events, or nodes in our Markov Chain. A scoring matrix is then generated with 439 columns and 439 rows, where the "START" row and "END" column are represented by the full stop. Running through every word in order, cumulatively increase the score in the index of [current_word, previous_word].

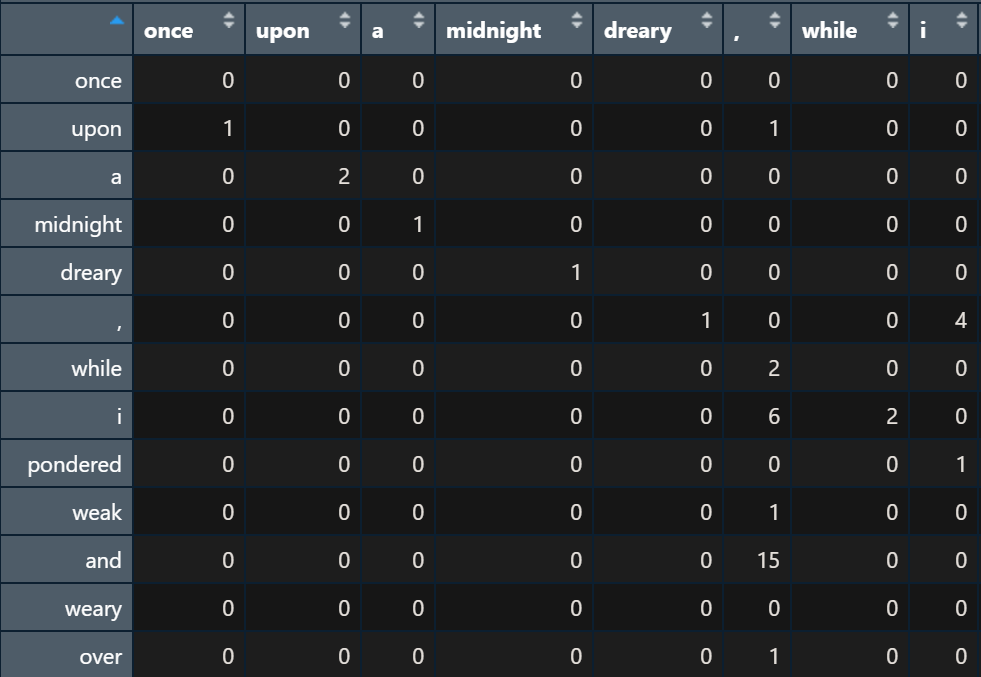
 We now have the model. To use this scoring matrix to generate new data, all we have to do is extract the full stop column, populate an array with all the non-zero events, duplicate the words as many times as they occur, then use a random number generator to choose a starting word. Find the starting word column index, find all the non-zero words that follow it, populate the array, randomly choose a word, and rinse and repeat until it chooses the terminating full stop. A simple "for" loop can generate as many sentences for the machine-generated poem as you'd like. My own generated 6-sentence stanza is as follows:

For the saintly days of forgotten lore, said I scarcely more.
For the fowl to borrow from off my chamber door.
Tell me what it wore, tapping, till the raven nevermore.
Take thy soul from thy crest be lifted, what thereat is I stood there and the dirges of evil.
Wretch, nevermore.
Quoth the raven, what it was unbroken.

 As you can probably read for yourself, it's not eloquent and it doesn't always make sense. Which is to be expected, it would be like asking a group of people to pass a paper around in a circle and make a legible sentence together if they only had knowledge of the single word the previous participant wrote. We can give the machine a better chance at writing its own poem if we let it see more of the previous event history, say a Second Order Markov Model. The concept is once again very similar, but with a second scoring matrix tracking the index of the current word, and the current-2 word. The methodology behind generating the sentence only changes in that the possibilities are narrowed down by only populating the array with words for which the previous two generated words exist. My new generated poem now looks more like this:

Prophet still, if bird or devil.
Till the dirges of his hope that melancholy burden bore of never-nevermore.
Till I scarcely more than muttered other friends have flown before.
This it is, on the morrow he will leave me, as a token of that one burden bore of never-nevermore.
Quaff this kind nepenthe and forget this lost lenore.
Quoth the Raven Nevermore.

 This looks already far more sophisticated! We can continue in this manner, but with such a small dataset the model will quickly become overtrained, allowing no possibility for new variance than the poem itelf.

Markov Model Simulator

 If you enjoyed this read and want to play around with Markov Models but have no desire to program your own, don't fear! I built a little simulator for you, take a look here:

Use Markov Models Here