What is an Enigma Machine?
The origins of the Enigma machine invention officially begins towards the end of the first world war in 1918, when Albert Scherbius cracked the puzzle that was rotor operated cipher machinery. He spent the next few years improving his prototype before securing the patent rights to a similar invention by Hugo Koch, unveiling the first publicly available Schreibende (Printing) Enigma in 1923. This machine would print out the encrypted message like a typewriter, however this made it too expensive for mainstream use and so one year later in 1924, the Enigma machine as we know it was created.
The new version, labelled Enigma A, showed its output on a series of glowlamps rather than paper, making it transportable and cheap. Despite being only 1/8th of the price of the prototype, it had its own issues. The main one being its lack of decoding function, along with the keyboard being sequential (ABCD...) instead of the more standard typewriter order (QWERT...). In 1926 these issues were ironed out with the release of the commercial Enigma machine (also refered to as model A26 or Enigma D) which is the version used by the majority of the German Army during World War 2.

How does it work?
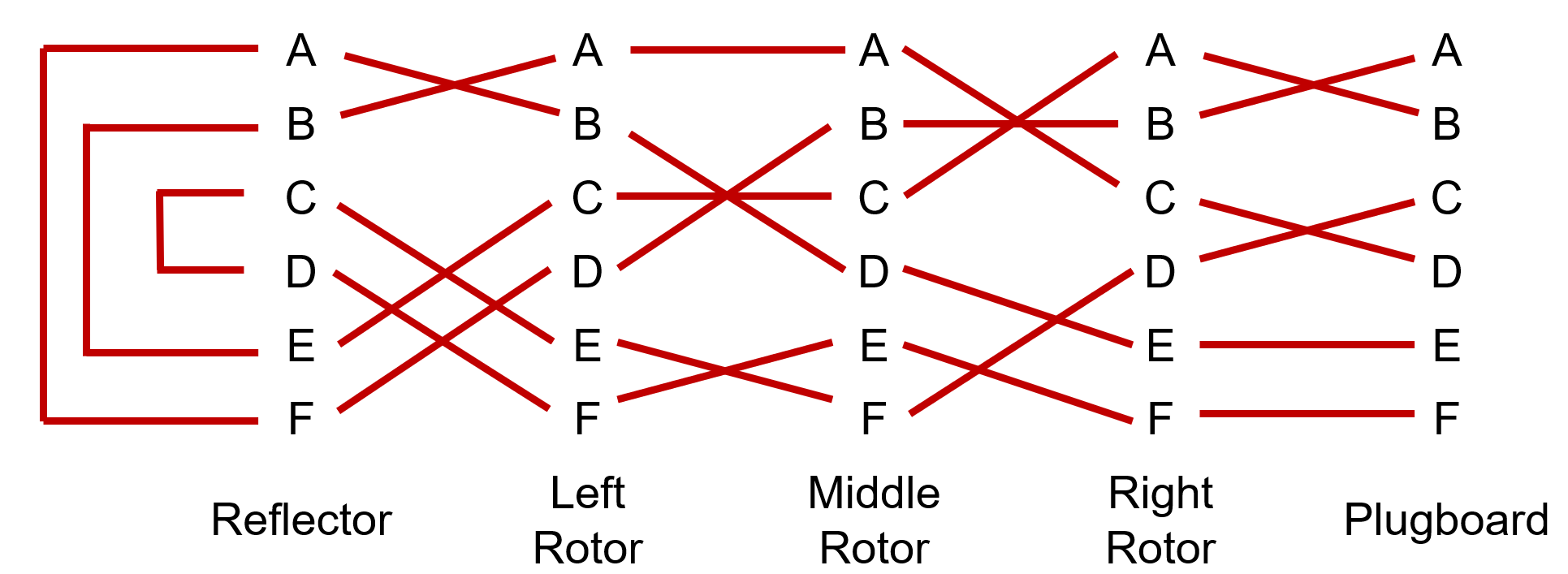
The brilliance of this particular cipher machine is in its simplicity, and the best method to understand how the machine functions is listing the individual components and their corresponding functions.
- Keyboard - QWERTY style input keyboard
- Steckerboard - A letter switching board, swapping the letter immediately upon input
- Rotors - A cog with each tooth corresponding to a letter, the wires in each cog would connect one tooth to another in a random pattern
- Reflector - a mirror which reflected the input signal back through the rotors
- Lampboard - A backlit keyboard which would light up the corresponding enciphered output letter
- Ground Setting - the rotor order at the beginning of input
The concept is simple: a letter key is pressed which sends an electrical signal down the wire, switching the input letter signal if it has a steckerboard swap for another static letter, before reaching the rotors. The signal would correspond to one tooth of the rotor cog which had a wire touching a tooth in a different position on the next cog, representing a virtual shift to another letter. As there are 3 cogs on the main model, there are 3 letter shift stages before the signal reaches the reflector which, as the name suggests, reflects the signal back into the cogs so the signal undergoes 3 more letter changes before arriving at the steckerboard once more. If the output letter has a stecker setting then it is swapped for its pair, before lighting up the final output letter on the lampboard.

The fast cog changes configurations with each key press, shifting by one tooth for each letter. Once it has undergone one full cycle, it will trigger the middle cog to shift by one tooth. When the middle cog has cycled fully, it will trigger a shift in the slow cog. The exception to these rules is the notches, each cog has a notch on one tooth that will cause an immediate shift in the next cog, causing a "double shift" step for the middle and slow cog. Generally the Right rotor was constructed to be the fast one, and the left rotor is considered as the slow one.

How did they crack it?
Due to the reflector, the Enigma machine is based on letter pairing. This means the result is a product of transpositions, such that typing 'A' will result in the letter 'D' and vice versa, so if two machines are set up with an identical initial state, then typing in the ciphertext will produce the original plaintext. The design of the reflector as a product of transposition by definition means that no letter can be encoded as itself, and this is the weakness used to crack it.
Every single day the Germans operators would be given a new set of global conditions as to the initial state their machines would be configured to. These were:
- Walzentage - which 3 of the 5 available rotors to use, and their order in the machine (slow - middle - fast)
- Steckerverbindungen - 6 pairs of letters that would be switched at the plugboard stage
- Grundstellung - the ground setting of the rotors, i.e. which letter/tooth of the cog was topmost
After initialising the machine, each message sent that day would have to be unique. In order to send a message the operator would select a random trigram of letters and run it through the machine twice to obtain 6 encoded letters. They would then reset the ground setting of the machine to the chosen random trigram and type out the rest of the message, thereby obtaining the complete ciphertext. This message would then be broadcast in Morse Code over the radio, which both the Germans and the Allies could hear.

| Rotor Order | III - I - II |
| Plug Connections | CG FI HZ JN QT RY |
| Ground Setting | VZW |
| Trigram | SLH SLH |
| Encoded Trigram | CKD GEC |
| Plaintext | "Hello there" |
| Ciphertext (Trigram Ground Setting) | YCTQDXVHHQ |
| Full Broadcast Message | CKD GEC YCTQDXVHHQ |
Looking at the machine itself, the design of it renders it almost impossible to guess the initial state of the Enigma machine in order to decipher the German messages. For example there are 5 rotors to choose from, and they can be placed in any order, so there are 5*4*3 = 60 total rotor combinations. The reflectors themselves are fixed and unchanging. The plugboard pairs up 12 letters, leaving 14 letters unchanged. The number of ways to switch a letter then becomes:
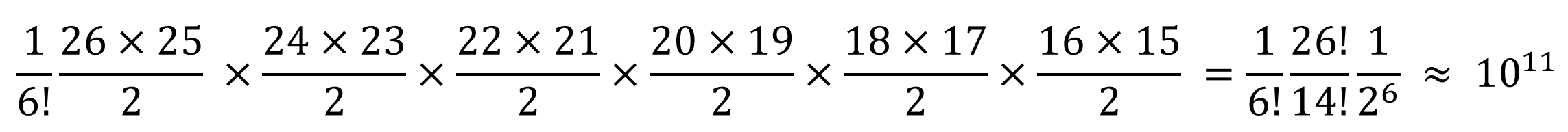
Each rotor can also be set on any of the 26 letters, so the total number of ground settings is 263. Putting all of this together, the total possible number of initial positions of the Enigma machine is:
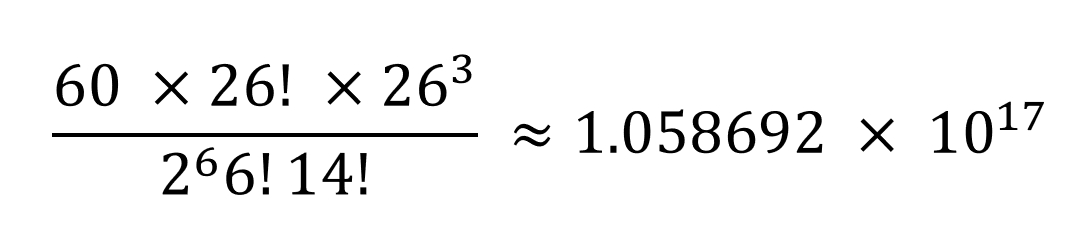
But it can be cracked, and a team consisting of 3 Polish scientists and 1 German spy did just that. In 1932 the Polish Cipher Bureaux hired Marian Rejewski, Jerzy Różycki, and Henryk Zygalski to work on the puzzle. Marian had access to an obsolete Enigma machine, but required help on the German daily initialisation routine which was provided by the French Intelligence. The French had succeeded in turning a German Cipher Office employee, Hans-Tilo Schmidt, into a spy for the Allies, who then provided the details they needed.

The first thing they did was write down the process of a letter being encoded as a sequence of permutations, where π is the plugboard, ρ1 is the fast rotor, ρ2 is the middle rotor, ρ3 is the slow rotor, and τ is the reflector.
With each key press at least one of the rotors will rotate, giving a different permutation combination.
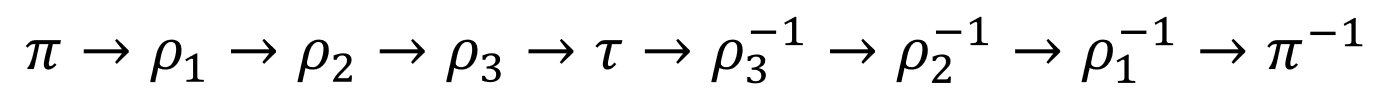
All the rotors and the reflector can then be compressed into σ, giving the full permutation π → σ → π-1 where σ and its inverse σ-1 are the same.
Representing this in the order right-to-left, and with σ changing with each step, the whole enciphering sequence set can be written as π-1σ1π, ... , π-1σnπ
Assume that an encrypted repeated trigram has been sent in Morse Code over a radiowave the allies can hear, and has been received as HSA PYT. It can then be deduced that the first letter of an unknown ciphertext makes an H on the first press when the machine is in the ground state, and a P three presses later. Using '*' to mark unknown plaintext, this can be represented as:
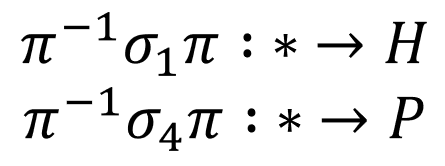
Using the fact the machine is symmetrical due to the reflector, then the reverse is also true, which we can write as:
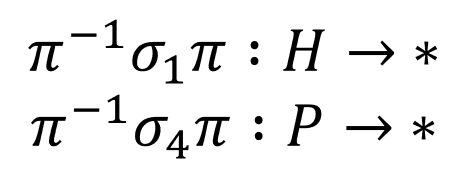
And these equations can be combined together to ultimately form:
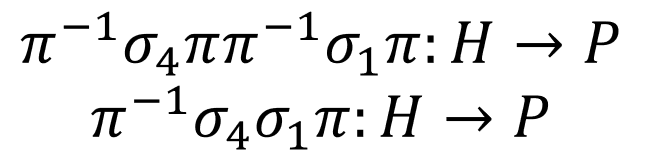
Many repeated trigrams will be used throughout the day, as the daily ground settings are used and this was the main form of communication. Assume the next repeated trigram sent is PPZ LEX, then we can repeat the previous steps to generate:
π-1σ4σ1π: P→L
We can combine the new sequence onto the old one to generate:
π-1σ4σ1π: H→P→L
Eventually, with enough messages and trigrams, multiple letter cycles will form containing all the letters of the alphabet. In this case it would be:
(H→P→L→T→K→G→B→D→U→H→...)(X→J→I→N→C→O→Q→V→E→X→...)(F→Y→F→...)(R→Z→R→...)(A)(M)(S)(W)
Which is two 9-cycles, two 2-cycles, and four 1-cycles, otherwise known as the characteristics of the day settings. These were catalogued and used to create Rejewski's Cyclometer, a device which finds the cycle structure for every possible rotor order and ground setting, a process which took roughly a year.

Inserting the cyle orders into the cyclometer would generate only 18 possible configurations for the rotor order and ground settings, however this cycle is only for the first letters of repeating trigrams. Repeating the process for the second and third letters of the trigram, generating two more cylce orders, and running them into the cyclometer would render only one possible configuration, which for this example is wheel order I=III-II, and ground setting FUQ. Knowing this, the Stecker combinations can be deduced. Assume the next message uses the encoded trigram GUH BIS, using the now known rotor order and ground setting it can be deciphered to YYY YLR. This strongly suggests the repeated trigram is YYY, so resetting the device and typing in YYY YYY should reveal the replaced letters. In this example the result would be GUH BZE, revealing the pairings Z→I, and E→S. Again, with enough messages and enough days, all the Stecker pairings, along with other daily settings, can be catalogued and referenced to speed up the process over time.
Officially the Polish team broke the Enigma Code in 1935, but the Germans realised their error in sending repeated trigrams and by 1940 they changed their protocols. This made Rejewski's characteristics obsolete, meaning the Enigma Machine had to be broken again, which Alan Turing et al. famously did at Bletchley Park, Milton Keynes.
